ГЛАВА 3. КОЛИЧЕСТВЕННАЯ ОЦЕНКА ИНФОРМАЦИИ

§ 3.1. ЭНТРОПИЯ   КАК   МЕРА   НЕОПРЕДЕЛЕННОСТИ   ВЫБОРА

 

 

§ 3.2  СВОЙСТВА ЭНТРОПИИ

 

Рассмотрим основные свойства энтропии, обратив внимание на то, что сформулированные условия для меры неопределенности выполняются.

1.  Энтропия является вещественной и неотрицательной величиной, так как для любого i(1) рi изменяется в интервале от 0 до 1, log pi отрицателен и, следовательно, — pi  log pi положительна.

2.  Энтропия — величина  ограниченная.   Для  слагаемых   - pi log pi  в  диапазоне  0<рi1   ограниченность очевидна. Остается определить предел, к которому стремится слагаемое — pi log pi, при рi—>0, поскольку — log pi при этом неограниченно возрастает:

Обозначив   a= 1/рi   и   воспользовавшись   правилом Лопиталя, получим

3.   Энтропия  обращается   в нуль лишь в том случае, если вероятность одного из состояний равна единице; тогда вероятности всех остальных состояний, естественно, равны нулю. Это   положение   соответствует случаю, когда состояние источника полностью определено.

4.    Энтропия   максимальна, когда все состояния источника равновероятны, что легко доказывается методом неопределенных множителей Лагранжа [23]:

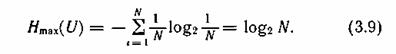
5. Энтропия источника и с двумя состояниями u1 и u2 изменяется от нуля до единицы, достигая максимума при равенстве их вероятностей:

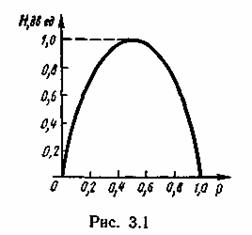
График зависимости H(U) в функции ρ

приведен на рис. 3.1. При ρ « (1- р)частная неопределенность, приходящаяся на состояние u1, велика, однако такие состояния источника весьма редки. Состояния u2 реализуются часто, но неопределенность, приходящаяся на такое состояние, очень мала. Поэтому энтропия, характеризующая среднюю неопределенность на одно состояние ансамбля, также мала. Аналогичная ситуация наблюдается при р » (1—р)·

Отметим, что энтропия непрерывно зависит от вероятностей отдельных состояний, что непосредственно вытекает из непрерывности функции - p log p.

6. Энтропия объединения нескольких статистически независимых источников информации равна сумме энтропии исходных источников.

§ 3.3. УСЛОВНАЯ ЭНТРОПИЯ  И ЕЕ СВОЙСТВА

 

При оценке неопределенности выбора часто необходимо учитывать статистические связи, которые в большинстве случаев имеют место как между состояниями двух или нескольких источников, объединенных в рамках одной системы, так и между состояниями, последовательно выбираемыми одним источником.

Определим энтропию объединения двух статистически связанных ансамблей U и V. Объединение ансамблей характеризуется матрицей p(UV) вероятностей р(uiui) всех возможных комбинаций состояний ui(1£ i £ N) ансамбля U и состояний uj(1 £ j £ k) ансамбля V:

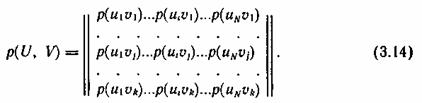
Суммируя столбцы и строки матрицы (3.14), получим информацию об ансамблях U и V исходных источников u и u:

Вероятности р(uiui) совместной реализации взаимозависимых состояний и, и ν·, можно выразить через условные вероятности р(ui/ui) или p(uj/ui) в соответствии с тем, какие состояния принять за причину, а какие — за следствие:

где p(ui/uj) — вероятность реализации состояний ui ансамбля U при условии, что реализовалось состояние uj ансамбля V; P(uj/ui) — вероятность реализации состояния uj ансамбля V при условии, что реализовалось состояние ui ансамбля U. Тогда выражение (3.11) для энтропии объединения принимает вид

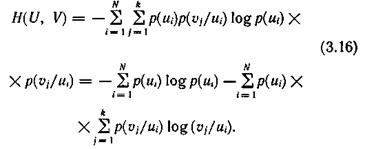
Сумма

представляет собой случайную величину, характеризующую неопределенность, приходящуюся на одно состояние ансамбля V при условии, что реализовалось конкретное состояние ui ансамбля U.

Назовем ее частной условной энтропией ансамбля  V и обозначим Hui(V):

При усреднении по всем состояниям ансамбля U получаем среднюю неопределенность, приходящуюся на одно состояние ансамбля V при известных состояниях ансамбля U:

или

Величину НU(V) называют полной условной или просто условной энтропией ансамбля V по отношению к ансамблю U.

§ 3.6. КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ

 

Передача информации инициируется либо самим источником информации, либо осуществляется по запросу. Она диктуется желанием устранить неопределенность относительно последовательности состояний, реализуемых некоторым источником информации. Обычно запрос обусловлен отсутствием возможности наблюдать состояния источника непосредственно. Поэтому абонент обращается к информационной системе, которая извлекает интересующую его информацию из источника посредством некоторого первичного преобразователя и направляет ее по каналу связи абоненту.

Информация проявляется всегда в форме сигналов. Сигналы z, поступающие с выхода первичного преобразователя источника информации на вход канала связи, принято называть сообщениями в отличие от сигнала u, формирующихся на входе линии связи. В зависимости от формы создаваемых сообщений различают источники дискретных и непрерывных сообщений.

Отдельные первичные сигналы с выхода источника дискретных сообщений называют элементами сообщения. Каждому элементу сообщения соответствует определенное состояние источника информации. В случае параллельной реализации источником информации множества состояний, как это имеет место, например, в документах с печатным текстом, первичный преобразователь, в частности, обеспечивает их последовательное отображение элементами сообщения. Таким преобразователем может быть как автоматическое читающее устройство, так и человек.

Основное понятие теории информации — количество информации — рассматривается в данном параграфе применительно к передаче отдельных статистически несвязанных элементов сообщения. Дискретный источник сообщений при этом полностью характеризуется ансамблем

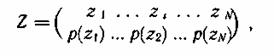
а непрерывный — одномерной плотностью распределения случайной величины — z— ρ(z). Особенности определения количества информации при передаче сообщений изложены в § 4.2.